[밑시딥] Chapter 2 퍼셉트론

단층 퍼셉트론

다수의 신호를 입력으로 받아 하나의 신호로 출력하는 것.

$x_1$, $x_2$ : 입력 신호

$y$ : 출력 신호

$w_1$, $w_2$ : 가중치

 

입력신호가 뉴런에 보내질 때 각각 고유한 가중치가 곱해진다.

뉴런에서 보내온 신호의 총합이 임계값(θ)을 넘어설 때만 1을 출력하며, 이는 뉴런을 활성화 한다고 표현하기도 한다.

식 2.1

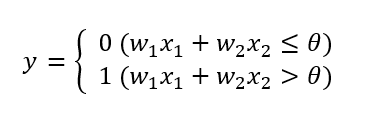
식 [2.1]의 $\theta$를 $-b$로 치환하면 퍼셉트론은 [식2.2]처럼 표현할 수 있음. 이는 기호 표기만 바꿨을 뿐, 의미는 같다. 여기에서 $b$를 편향이라고 한다.

퍼셉트론은 입력 신호에 가중치를 곱한 값과 편향을 합하여, 그 값이 0을 넘으면 1을 출력하고, 그렇지 않으면 0을 출력한다.

---

단순한 논리 회로

1. AND 게이트

두 입력이 모두 1일 때만 1을 출력, 그 외에는 0을 출력

AND의 진리표

AND 게이트를 퍼셉트론 표현하기 위해서는 $w_1$, $w_2$, θ의 값을 조정하면 된다.

ex) ($w_1$, $w_2$, θ) 가 (0.5, 0.5, 0.7)

 

2. NAND 게이트

Not And로 AND 게이트를 뒤집은 결과가 나옴. 두 입력이 모두 1일 때만 0을 출력, 그 외에는 1을 출력

NAND의 진리표

ex) ($w_1$, $w_2$, θ) 가 (-0.5, -0.5, -0.7)

 

3. OR 게이트

입력 신호 중 하나라도 1이면 1을 출력, 그 외에는 0을 출력

OR의 진리표

ex) ($w_1$, $w_2$, θ) 가 (0.5, 0.3, 0.4)

 

AND, NAND, OR 게이트는 모두 퍼셉트론으로 표현 가능하다.

Q : 그렇다면 표현 못하는 것이 존재할까?

A : XOR 게이트

 

4. XOR 게이트 

배타적 논리합으로, 입력 신호 중 하나만 1일 때만 1을 출력

XOR의 진리표

식 2.1의 퍼셉트론은 직선으로 두 영역을 나눈다. 직선으로 나뉜 한쪽을 1, 다른 쪽은 0으로 출력한다.

아래 그래프에서 회색 영역은 0을, 다른 영역은 OR 게이트의 성질을 만족하여 1을 출력한다. 

AND, NAND, OR은 모두 왼쪽 사진처럼 한 직선으로 나눌 수 있다.

하지만 오른쪽 XOR 그래프는 하나의 직선으로 구분할 수 없기 때문에 퍼셉트론으로 표현하지 못한다는 한계가 존재한다.

 

Q :그렇다면 XOR는 퍼셉트론으로 표현을 못할까?

A : 다층 퍼셉트론을 이용하면 됨

---

다층 퍼셉트론

퍼셉트론을 여러개를 쌓는 것

앞서 XOR는 퍼셉트론으로 표현을 하지 못하지만, 다층 퍼셉트론으로 표현할 수 있다고 했음.

이는 XOR를 AND, NAND, OR의 조합으로 표현하면 퍼셉트론으로 표현할 수 있다는 의미.

 

사실 XOR의 진리표는 다음과도 표현할 수 있다.

$s_1$ : 두개의 입력을 NAND한 결과

$s_2$ : 두개의 입력을 OR한 결과

NAND와 OR로 표현한 XOR의 진리표

$s_1$과$s_2$ AND하면 XOR을 표현할 수 있다.

 

XOR의 퍼셉트론은 다음 그림과 같다.

XOR의 퍼셉트론

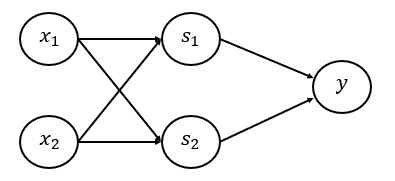
이처럼 층이 여러개인 퍼셉트론을 다층 퍼셉트론이라 한다.

---

참고 

SDRLurker/deep-learning: '밑바닥부터 시작하는 딥러닝' 공부한 내용을 jupyter notebook으로 정리하였습니다. (github.com)

nbviewer.jupyter.org/github/SDRLurker/deep-learning/blob/master/%EB%AA%A9%EC%B0%A8.ipynb

Jupyter Notebook Viewer