| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- vscode
- LeetCode
- 백준 A와 B
- 두 포인터
- 브루트포스
- 백준
- 파이썬
- 프로그래머스 길찾기 게임
- 학습 완료 알람
- 백트래킹
- git 사용자 설정
- 사과 장수
- 12904 파이썬
- 프로그래머스 사과 장수
- 백준 극장 좌석
- 투포인터
- 12904 python
- 2302 파이썬
- 2583 python
- 백준 12904
- slack webhook
- 2583 파이썬
- 백준 2853
- 2302 python
- 2853 파이썬
- 2853 python
- docker
- 백준 2470
- 모델 완료 알람
- 백준 배
- Today
- Total
bbooo
[밑시딥] 부록 Softmax-with-Loss 계층의 계산 그래프 본문
소프트맥스 함수와 교차 엔트로피 오차의 계산 그래프를 그려보고, 그 역전파를 구해보자
소프트맥스 함수는 'softmax' 게층, 교차 엔트로피 오차는 'Cross Entropy Error' 계층, 이 둘을 조합한 계층을 'softmax-with-Loss'계층이라 한다.
0. 교차 엔트로피 오차의 계산 그래프의 개요

그림 3-1에서는 3클래스 분류를 수행하는 신경망을 가정하고 있다.
Softmax의 입력 : $(a_1 , a_2 , a_3)$
Softmax의 출력 : $(y_1, y_2, y_3)$
Cross Entropy Error의 정답 레이블 : $(t_1, t_2, t_3) $
Cross Entropy Error의 출력 : 손실 $L$
Softmax와 Cross Entropy Error에 관한 설명은 뒤에 이어서 하겠음.
1. 순전파
[그림 A-1]의 계산 그래프에서는 Softmax계층과 Cross Entropy Error 계층의 내용을 생략했었다.
이 두 계층의 내용을 생략하지 않고 그려보자.
소프트 맥스 함수는 입력 $(a_1 , a_2 , a_3)$ 를 정규화 하여 $(y_1, y_2, y_3)$을 출력하는 함수이다.
$$y_k = \frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i)} = \frac{입력신호 a_k의 지수함수}{모든 입력신호의 지수함수 값의 합}$$

[그림 A-2] Softmax 계층의 계산 그래프이다.
$(a_1 , a_2 , a_3)$를 입력받아 $(y_1, y_2, y_3)$을 출력한다.
이어서 Cross Entropy Error 계층을 보자.
교차 엔트로피 오차는 softmax의 출력 $(y_1, y_2, y_3)$와 정답레이블 $(t_1, t_2, t_3) $을 입력받아 손실 Loss를 계산하는 손실함수이다.
$$ L = -\sum_{k}^{}t_klogy_k $$
$y_k$ : 신경망의 출력값
$t_k$ : 정답 레이블
이 때 log는 밑이 $e$인 자연로그임을 주의하자.

[그림 A-3]은 Cross Entropy Error 계층의 계산 그래프이다.
순전파 계산은 특별히 어렵지 않으므로, 역전파를 살펴보겠다.
2. 역전파
역전파를 계산하기 전에, 이전에 배웠던 역전파를 기억해보자.


Cross Entropy Error 계층의 역전파부터 보자. 이 계층의 역전파는 [그림 A-4]처럼 그릴 수 있다.

이 계산 그래프의 역전파를 구할 때는 다음을 유념해야 한다.
- 역전파의 초기값, 즉 [그림 A-4]의 가장 오른쪽 역전파의 값은 1이다. $\frac{\vartheta L}{\vartheta L} = 1$ 이므로
- 'X'노드의 역전파는 순전파 시 입력들의 값을 서로 바꿔 상류의 미분에 곱하고 하류로 흘린다.
- '+'노드에서는 상류에서 전해지는 미분을 그대로 흘린다
- 'log'노드의 역전파는 다음 식을 따른다
$$y = logx$$
$$\frac{\vartheta y}{\vartheta x} = \frac{1}{x}$$
[A-4]에서 $ \frac{\vartheta L}{\vartheta y_1}$ 을 계산해보면 다음과 같다.
$$\frac{\vartheta L}{\vartheta y_1} = upstream * Local$$
$$ = -t_1 * \frac{dlog y_1}{dy_1} $$
$$= -t_1 * \frac{1}{y_1} = - \frac{t_1}{y_1}$$
Cross Entropy Error 계층의 역전파 결과는 $ (-\frac{t_1}{y_1},-\frac{t_2}{y_2},-\frac{t_3}{y_3})$ 이며, 이 값이 Softmax 계층으로의 역전파 입력이 된다.
Softmax 계층의 역전파를 한단계씩 확인해보자

앞 계층(Cross Entropy Error 계층)의 역전파 값이 흘러들어옴.

순전파 계산 결과 $ y_1 = \frac{exp(s_1)}{S} $에 따라 다음 계산이 이뤄진다.
$$ -\frac{t_1}{y_1}exp(a_1) = -t_1*\frac{1}{y_1}*exp(a_1) $$
$$ = -t_1*\frac{S}{exp(a_1)}*exp(a_1) $$
$$ = -t_1S $$
동일하게 $ -t_2S, -t_3S$ 를 구할 수 있다.

나눗셈 역전파에서는 다음 계산이 이루어진다.
$$ 상류값 * -(순전파때 출력)^2 $$
순전파 때 $exp(a_1)$은 여러 갈래로 나뉘어 흘렀다. 역전파 때는 그 반대로 흘러온 여러 값을 더하기 때문에, 상류값은 다음과 같이 계산한다.
$$ (-t_1S) + (-t_2S) + (-t_3S) = -S(t_1 + t_2 + t_3) $$
순전파 때의 출력은 $\frac{1}{S}$이므로 역전파를 식은 다음과 같다.
$$ -S(t_1 + t_2 + t_3) * -\frac{1}{s^2} $$
여기서 $ (t_1 , t_2, t_3) $ 는 '원-핫 벡터'로 표현된 정답 레이블이다.
따라서 $ (t_1 + t_2 + t_3) = 1 $이 되므로 다음과 같이 표현될 수 있다.
$$ -S(t_1 + t_2 + t_3) * -\frac{1}{s^2}
= \frac{(t_1+t_2+t_3)}{S} = \frac{1}{S} $$

'+'노드이므로 입력을 그대로 출력한다.

'x'노드는 입력을 서로 바꿔 곱한다.
Downstream gradients = Local gradients * Upstream gradient 에 따라 다음 식이 나온다
$$-\frac{t_1}{y_1}\frac{1}{S} $$
$ y_1 = \frac{exp(s_1)}{S} $ 이기 때문에 다음과 같이 정리할 수 있다.
$$ -\frac{t_1}{y_1}\frac{1}{S}
= -t_1*\frac{S}{exp(a_1)}*\frac{1}{S} $$
$$ =\frac{-t_1}{exp(a_1)} $$
동일하게 $ =\frac{-t_2}{exp(a_2)} $와 $ =\frac{-t_3}{exp(a_3)}$ 을 구할 수 있다.

'exp'노드에서는 다음 관계식이 성립된다.
$$y = exp(x) $$
$$ \frac{\vartheta y}{\vartheta x} = exp(x) $$
두 갈래의 입력의 합에 $exp(a_1)$을 곱하면 여기서 구하는 역전파 값이 나온다.
$$ (\frac{1}{S} - \frac{t_1}{exp(a_1)})exp(a) = \frac{exp(a_1)}{S} - t_1 $$
$ \frac{exp(a_1)}{S} = y_1 $이기 때문에 위 식을 다음과 같이 정리될 수 있다.
$$ y_1 - t_1 $$
나머지 $ y_2 - t_2$ 와 $ y_3 - t_3 $ 도 동일하게 구할 수 있다.
3. 정리
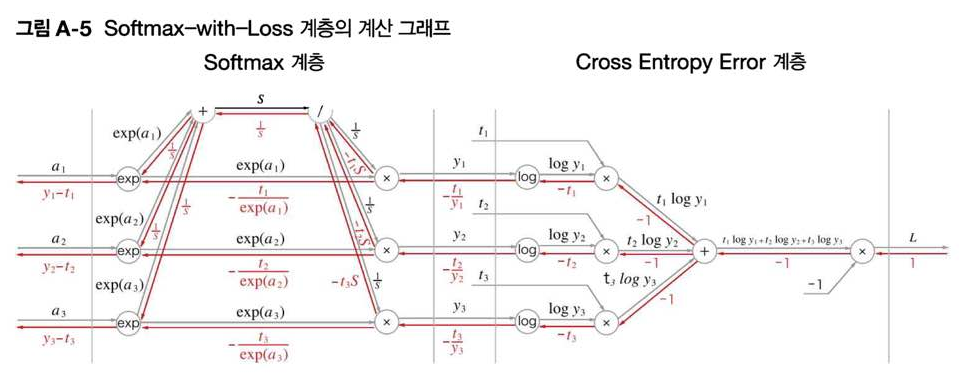
모든 순전파 값과, 역잔파 값을 채우면 [그림 A-5]와 같이 구성된다.
'SSAC X IFFEL > 밑바닥 부터 시작하는 딥러닝' 카테고리의 다른 글
| [밑시딥] Chapter 2 퍼셉트론 (1) | 2021.01.25 |
|---|

